arc of the upper half of cardioid r=a(1-cos@) is bisected at @=2π/3. perimeter of the curve is 8a
Published 2 days ago • 34 plays • Length 10:11Download video MP4
Download video MP3
Similar videos
-
11:54
show that the arc of the uppper half of the curve r=a(1-cosθ) is bisected at θ=2π/3.
-
32:06
#05 rectification | arc length | perimeter of cardiod r=a(1 cos θ)show that θ=π/3 divide upper half
-
11:27
arc length of cardioid r=a(1 cos@). point on with vectorial angle π/3, is middle point of upper half
-
18:47
show that arc of the upper half of the curve r=a(1-cosθ) is bisected by θ=2π/3.
-
36:14
integral calculus: rectification part-(v)
-
![arc length of a cardioid! [ using a polar coordinate system ]](https://i.ytimg.com/vi/HqoqjM8ouAc/mqdefault.jpg)
8:38
arc length of a cardioid! [ using a polar coordinate system ]
-
11:32
how to find arc length and sector area of circles | geometry
-
21:05
why is there no equation for the perimeter of an ellipse‽
-
7:57
arc length (formula explained)
-
6:58
find the perimeter of the cardioid r=a(1 cos theta)#speakwithmath
-
5:52
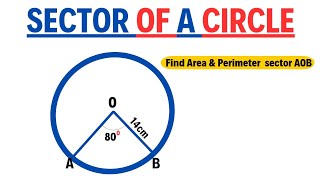
how to find the area and perimeter of a sector of a circle
-
2:11
a-level further maths g2-11 polar curves: cardioid r=a(1 cosθ)
-
10:44
#11 rectification engineering mathematics 2 hindi { find the perimeter of cardioid }
-
0:39
geometry problem - find the perimeter of the arc.
-
5:27
calculus help: arc length of cardioid: consider the curve which looks like c: r=3θ^2 where 0≤θ≤2π
-
9:01
find the perimeter of the cardioid r=a(1-cos theta)#speakwithmath
-
10:52
find the perimeter of the cardioid r=a(1-cosθ)
-
0:27
how to get the area and arc length of a sector #shorts #tutorial #formula
-
5:34
find the perimeter of the curve r=a.cosθ (b.sc.mathematics:integral calculus:rectification)
-
10:02
length of the arc of the parabola l/r=1 cos@ cut off by its latus rectum is l{√2 log(1 √2)}
-
10:16
arc length: perimeter of an ellipse | lecture 36 | vector calculus for engineers
-
9:38
parametric arc length, simpson's rule (kristakingmath)