calculus help: find the arc length of the curve y=1/8 (-x^2 8lnx) from x=4 to x=6 - integration
Published 2 years ago • 863 plays • Length 3:49Download video MP4
Download video MP3
Similar videos
-
9:36
calculus help: find the arc length of the circle by integral (x-1)^2 (y-3)^2=16 - integration
-
4:41
calculus help: arc length - the lengths of the following curves - x=(y/7)^2-49/8 ln(y/7) ,6≤y≤30
-
30:47
arc length calculus problems,
-
2:48
calculus help: find the arc length: application of integration: y=1/2 x^2-1/4 lnx from x=1 to x=e
-
5:00
arc length - integration: find the length of the curve y=(4-x^(2/3) )^(3/2) from x=1 to x=8
-
3:57
calculus help: the arc length and how to answer - techniques
-
3:26
calculus help: find the arc length: application of integration: 6xy=x^4 3 from x=1 to x=2
-
2:14
calculus help: find the exact arc length of the curve x = cos4t 12, y = sin4t - 5 on the interval
-
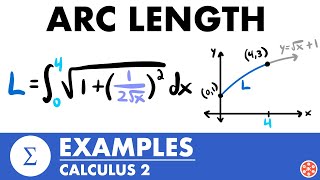34:33
arc length examples | calculus 2 - jk math
-
16:21
find the arc length of a function with calculus
-
29:00
calculus 2 ( ch8 ) arc length
-
![calculus help: determine the arc length of f(x)=(x/2)^(3/2) of [0;2] - techniques - integrations](https://i.ytimg.com/vi/t-f8D9TKxV4/mqdefault.jpg)
2:58
calculus help: determine the arc length of f(x)=(x/2)^(3/2) of [0;2] - techniques - integrations
-
3:52
calculus help: find the arc length of y=2x^(3/2) on 1≤x≤3 - integration - techniques
-
3:03
calculus help: find the arc length of the function f(x)=2/3 (x^2 1)^(3/2) on the interval 0≤x≤1
-
4:30
calculus help: arc length - x=y^4/4 1/(8y^2 ) , 1≤y≤2 - application of integrations - solved!!!
-
3:29
calculus help: integral techniques: find the arc length y=1/2 ( e^x e^(-x) ) from x=0 to x=1
-
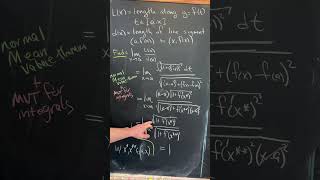0:58
an arclength limit
-
4:20
calculus: find the arc length of the graph of the function over the indicated interval. y=4x^3/2 9
-
0:53
length of a curve. #math #animation #integral #calculus
-
2:24
find the arc length of the graph of the function over the indicated interval. y=1/2 (e^x e^(-x))
-
2:31
application of integration: find the area between the curve g(x)=x^3- 0.25x^4 and the line f(x)=2x-8
-
2:24
calculus help: integral of arc length with contour integral: evaluate ∫c yds,c :x=t^2,y=t,−1≤t≤7