compute the are length exactly. y=1/8 x^4 1/4 x^2,-2 ≤x ≤-1
Published 1 month ago • 10 plays • Length 0:33
Download video MP4
Download video MP3
Similar videos
-
 0:33
0:33
find the exact arc length of the curve over the interval. x=1/8 y^4 1/4 y^-2 …
-
 0:33
0:33
find the exact arc length of the curve x = 1/8*y^4 1/4*y^(-2) from y = 1 to y = 4.
-
 0:33
0:33
find the exact length of the curve. y = 1 - e^-x , 0 ≤x ≤2
-
 0:33
0:33
use the arc length formula to find the length of the curve y = 4x - 1, -3 ≤ x ≤ 2. check your a…
-
 0:33
0:33
in exercises 49–56, find the arc length of the curve on the given interval. x=arcsint, y=ł…
-
 6:34
6:34
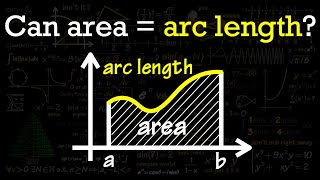
area under the curve equals to the arc length?
-
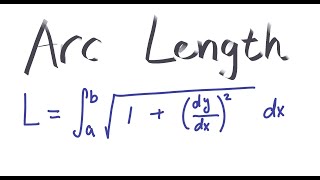 17:52
17:52
how to find arc length/length of curve - detailed example showing full step by step solution
-
 0:33
0:33
(a) find the arc length function for the curve y=ln(sinx), 0xπ, with starting point (π/ …
-
 0:33
0:33
for the following exercises, find the exact arc length for the following problems over the given in…
-
 0:33
0:33
arc length find the length of the curve y=ln(cosx), 0 ≤x ≤π/ 3
-
 0:33
0:33
9-20 find the exact length of the curve. x=1/3 √(y)(y-3), 1 ⩽y ⩽…
-
 0:33
0:33
arc length in exercises 49-54, find the arc length of the curve on the given interval. \beginarray…
-
![use the arc length formula [3] to find the length of the curve y=2 x-5,-1 ⩽x ⩽3 .…](https://i.ytimg.com/vi/j72yieFQvLU/mqdefault.jpg) 0:33
0:33
use the arc length formula [3] to find the length of the curve y=2 x-5,-1 ⩽x ⩽3 .…
-
 0:33
0:33
9-20 find the exact length of the curve. y=√(x-x^2) sin^-1(√(x))
-
 0:33
0:33
find the are length parameter along the curve from the point where t=0 by evaluating the integral s…
-
 0:33
0:33
find the length of one arch of the cycloid x=θ-sinθ, y=1-cosθ
-
 0:33
0:33
find the length of the curve. r(t) = i t^2 j t^3 k , 0 ≤t ≤1
-
 0:33
0:33
finding arc length in exercises 17-26, (a) sketch the graph of the function, highlighting the part …
-
 0:33
0:33
express the arc length of the curve y=x^4 between x=2 and x=6 as an integral (but do not evaluate…
-
 0:33
0:33
use eq .(4) to compute the arc length of y=ln(e^x 1/e^x-1) over […
-
 0:33
0:33
37-40 set up an integral that represents the length of the curve. then use your calculator to find …
-
 0:33
0:33
express the exact arc length of the curve over the given interval as an integral that has been simp…
Clip.africa.com - Privacy-policy
 0:33
0:33
 0:33
0:33
 0:33
0:33
 0:33
0:33
 0:33
0:33
 6:34
6:34
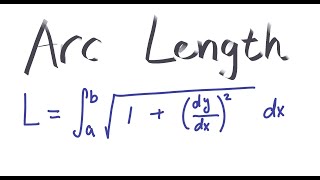 17:52
17:52
 0:33
0:33
 0:33
0:33
 0:33
0:33
 0:33
0:33
 0:33
0:33
![use the arc length formula [3] to find the length of the curve y=2 x-5,-1 ⩽x ⩽3 .…](https://i.ytimg.com/vi/j72yieFQvLU/mqdefault.jpg) 0:33
0:33
 0:33
0:33
 0:33
0:33
 0:33
0:33
 0:33
0:33
 0:33
0:33
 0:33
0:33
 0:33
0:33
 0:33
0:33
 0:33
0:33