evaluate lim(x→π/2) (2xtanx-πsecx) || limit x tend pi/2 [2xtanx-πsecx] | ∞-∞ form indeterminate form
Published 2 days ago • 39 plays • Length 6:44Download video MP4
Download video MP3
Similar videos
-
4:14
evaluate lim(x→0) xtan(pi/2-x) || limit x tend to 0 xtan(pi/2 -x) indeterminate form
-
7:08
evaluate lim(x→π/2) ln(x−π/2)/tan(x) || limit x tend pi/2 log(x-pi/2)/tanx indeterminate form
-
![evaluate lim(x →∞) 2^x sin(a/2^x) || limit x tend to infinity 2^(x)sin(a/2^x) [ 0.∞ form ]](https://i.ytimg.com/vi/uwlzBX-F1Yw/mqdefault.jpg)
10:29
evaluate lim(x →∞) 2^x sin(a/2^x) || limit x tend to infinity 2^(x)sin(a/2^x) [ 0.∞ form ]
-
5:59
evaluate lim(x→2) (2-x)tan(πx/4) || limit x tend to 2 (2-x)tan(πx/4) indeterminate form ( 0.∞ form )
-
![evaluate lim(x→1) sec(pi/2x)logx || limit x tend to 1 sec(π/2x)logx indeterminate form [ 0.∞ form ]](https://i.ytimg.com/vi/m-7y0PxT3q8/mqdefault.jpg)
6:44
evaluate lim(x→1) sec(pi/2x)logx || limit x tend to 1 sec(π/2x)logx indeterminate form [ 0.∞ form ]
-
28:16
let's do complex analysis: integrating sin^2(x)/x^2(x^2 1) from 0 to infinity using residue theorem
-
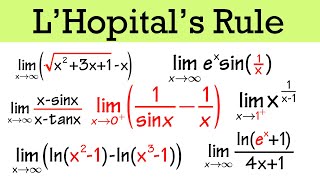44:56
l'hopital's rule ultimate study guide
-
15:59
lim sin(x)/x = 1 as x goes to 0
-
0:14
the limit is the limit is the limit is the limit
-
![evaluate lim(x→0) (1/x^2)-(1/xtanx) || limit x tend to 0 (1/x^2 -1/xtanx) [ ∞-∞ indeterminate form]](https://i.ytimg.com/vi/j58YjwpuYOk/mqdefault.jpg)
6:27
evaluate lim(x→0) (1/x^2)-(1/xtanx) || limit x tend to 0 (1/x^2 -1/xtanx) [ ∞-∞ indeterminate form]
-
11:27
evaluate lim(x→2) (1/(x-1)-1/log(x-1)) || limit x tend to 2 (1/(x-1) -1/log(x-1)) indeterminate form
-
5:32
evaluate : lim x → π/2 (π/2 - x)tanx
-
0:23
how to find the limit of the square root of x as x approaches infinity #shorts
-
8:40
evaluate lim(x→1) x/(x-1)-(1/logx) || limit x tend to 1 x/(x-1)-1/logx | ∞-∞ form indeterminate form
-
11:20
prove that lim(2^n xn) converges where x0 = x, xn 1 = xn / (1 sqrt(1 xn^2)) (iliekmathphysics
-
5:05
evaluate lim (x→0) (e^x e^-x - 2) / x²
-
5:13
evaluate lt (2-x/a)^tan(π/2a) as x tends to a
-
4:52
(sinx)^tanx as x tends to infinity
-
3:04
find the limit of (2 - x^2)/(x^2 x - 1) as x approaches infinity
-
5:07
evaluate: lim(x→pi/2) tanx/tan3x
-
1:40
learn how to evaluate a limit at infinity
-
20:20
calculus 1 - introduction to limits