find x, y, n if 2nd, 3rd, 4th terms in expansion of (x y)^n are 240, 720, 1080 respectively.
Published 12 years ago • 6.4K plays • Length 6:13
Download video MP4
Download video MP3
Similar videos
-
 6:47
6:47
if 2nd, 3rd and 4th tems in the expansion of `(x y)^n` be 240,720 and 1080 respectively, find x,...
-
 11:05
11:05
the second, third and fourth terms in the binomial expansion `(x a)^n`are 240, 720 and 1080,
-
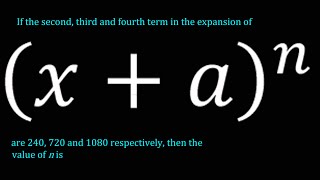 3:48
3:48
if the second, third and fourth term in the expansion of (x a)^n are 240, 720 and 1080 respectively,
-
 19:00
19:00
if the 2nd,3rd and 4th term in expansion of (a x)^n are 240, 720,1080, then find a,x and n
-
 9:56
9:56
xi binomial theorem the second, third and fourth term in the binomial expansion x a^n are 240, 720 a
-
 30:11
30:11
binomial theorem expansion, pascal's triangle, finding terms & coefficients, combinations, algebra 2
-
 8:26
8:26
binomial theorem - general formula | don't memorise
-
 8:37
8:37
how to evaluate binomial coefficients
-
 13:15
13:15
binomial theorem | polynomial and rational functions | algebra ii | khan academy
-
 7:52
7:52
the second, third and fourth terms in the binomial expansion `(x a)^n` are 240, 720 and 1080, re...
-
 15:26
15:26
if the 2,3,4 th terms in the. expansion of (a x)ⁿ are respectively 240,720,1080 find a,x,n
-
 11:09
11:09
binomial theorem | 7 marks problem @eag
-
 5:00
5:00
binomial theorem find term independent of variable x
-
 7:29
7:29
the second third and fourth terms in the binomial expansion (x a)^n | binomial theorem example 8
-
 0:54
0:54
find the coefficient of a specific term in a binomial expansion
-
 12:02
12:02
nth term of binomial expansion | general formula
-
 1:00
1:00
finding remainder using binomial theorem | frequently asked problems in jee exam | jee main 2023/24
-
 1:01
1:01
tips on expanding a binomial using pascal’s triangle
-
 7:06
7:06
if the 2nd, 3rd and 4th terms in the expansion of ltmath gt ltmrow gt ltmsup gt ltmrow
-
![find the 13th term in expansion of [9x - 1/{3*sqrt(x)}] raised to power 18.](https://i.ytimg.com/vi/Py71jrBDZCc/mqdefault.jpg) 1:42
1:42
find the 13th term in expansion of [9x - 1/{3*sqrt(x)}] raised to power 18.
-
 11:08
11:08
binomial expansion | a-level and ib | addvance maths 😊➕
-
 22:38
22:38
the binomial theorem | binomial expansion | how to find the kth term of a binomial expansion
Clip.africa.com - Privacy-policy
 6:47
6:47
 11:05
11:05
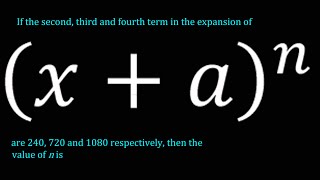 3:48
3:48
 19:00
19:00
 9:56
9:56
 30:11
30:11
 8:26
8:26
 8:37
8:37
 13:15
13:15
 7:52
7:52
 15:26
15:26
 11:09
11:09
 5:00
5:00
 7:29
7:29
 0:54
0:54
 12:02
12:02
 1:00
1:00
 1:01
1:01
 7:06
7:06
![find the 13th term in expansion of [9x - 1/{3*sqrt(x)}] raised to power 18.](https://i.ytimg.com/vi/Py71jrBDZCc/mqdefault.jpg) 1:42
1:42
 11:08
11:08
 22:38
22:38