given the matricesa=\begin{bmatrix}1& -1&2 \\3&4&5\\0&1&-1 \end{bmatrix} ... | plainmath
Published 2 years ago • 70 plays • Length 10:59Download video MP4
Download video MP3
Similar videos
-
 5:58
5:58
consider the matricesa=\begin{bmatrix}1 & -1 \\0 & 1 \end{bmatrix},b=\begin{bmatrix} ... | plainmath
-
 3:18
3:18
given the matricesa=\begin{bmatrix}-1 & 3 \\2 & -1 \\ 3&1 \end{bmatrix} \text{ and } ... | plainmath
-
 9:56
9:56
given the two matrices,a=\begin{bmatrix}1 & 2&3 \\1 & 1&2\\0&1&2 \end{bmatrix} ... | plainmath
-
 6:12
6:12
a=\begin{bmatrix}2& 1&1 \\-1 & -1&4 \end{bmatrix}b=\begin{bmatrix}0& 2 \\-4 & 1\\2 ... | plainmath
-
 3:18
3:18
let a=i_2 and b=\begin{bmatrix}1 & 1 \\0 & 1 \end{bmatrix} . discuss the validity of ... | plainmath
-
 1:31
1:31
given the matricesa=\begin{bmatrix}5 & 3 \\ -3 & -1 \\ -2 & -5 \end{bmatrix} \text ... | plainmath
-
 8:01
8:01
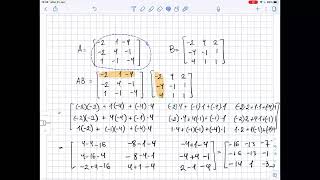
if a=\begin{bmatrix}-2 & 1&-4 \\-2 & 4&-1 \\ 1 &-1 &-4 \end{bmatrix} \text{ and } ... | plainmath
-
 7:08
7:08
linear algebra - matrix operations
-
 3:01:28
3:01:28
greg yang | large n limits: random matrices & neural networks | the cartesian cafe w/ timothy nguyen
-
![finding a matrix given it's eigenspaces [passing linear algebra]](https://i.ytimg.com/vi/j3YK3V7_2ok/mqdefault.jpg) 5:02
5:02
finding a matrix given it's eigenspaces [passing linear algebra]
-
 4:28
4:28
find if possible the matrices:a. ab b. ba.a=\begin{bmatrix}1 & -1&4 \\4 & -1&3\\2& ... | plainmath
-
 2:31
2:31
compute the indicated matrices, if possible .a^2blet a=\begin{bmatrix}1 & 2 ... | plainmath
-
 5:02
5:02
let a=\begin{bmatrix}2 & -1&5 \\-3 & 4&0 \end{bmatrix} \text{ and } b=\begin{bmatrix ... | plainmath
-
 4:31
4:31
use the graphing calculator to solve if possiblea=\begin{bmatrix}1 & 0&5 \\1 & -5&7 ... | plainmath
-
 3:59
3:59
find the following matrices:a) a b.(b) a - b.(c) -4a.a=\begin{bmatrix}2 & -10&-2 ... | plainmath
-
 4:34
4:34
find if possible the matrices:a) ab b) ba.a=\begin{bmatrix}3 & -2 \\ 1 & 5 \end ... | plainmath
-
 5:16
5:16
verify that (ab)^t = b^ta^tif a=\begin{bmatrix}2 & 1 \\ 6 & 3 \\ -2&4 \end{bmatrix ... | plainmath
-
 9:37
9:37
show that a and b are not similar matricesa=\begin{bmatrix}1 & 0 &1 \\ 2 & 0 &2 \\ ... | plainmath
-
 3:34
3:34
a=\begin{bmatrix}4 & 0 \\0 & -6 \end{bmatrix} , b=\begin{bmatrix}0 & -3 \\3 & -3 \end... | plainmath
-
 2:20
2:20
solve for x in the equation, given3x 2a = ba=\begin{bmatrix}-4 & 0 \\1 & -5\\-3&2 ... | plainmath
-
 4:50
4:50
find the least-square solution of ax=b , wherea=\begin{bmatrix}1& -2 \\-1 & 2\\0&3\ ... | plainmath
-
 2:07
2:07
find the products ab and ba for the diagonal matrices.a=\begin{bmatrix}2 & 0 \\0 & ... | plainmath