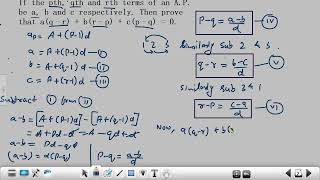
if the pth, qth and rth terms of an a.p be a, b and c respe, then prove that a(q-r) b(r-p) c(p-q)=0
Published 11 months ago • 34 plays • Length 13:11
Download video MP4
Download video MP3
Similar videos
-
 9:12
9:12
the pth qth and rth terms of an ap are a b c respectively show that (q-r)a (r-p)b (p-q)c=0
-
 5:27
5:27
if pth, qth and rth terms of an a.p. are a, b, c respectively, then show that a(q-r) b(r-p) c(p-q)=0
-
 7:21
7:21
if the pth, qth and rth term of an ap be a,b and c respectively, show that a(q-r) b(r-p) c(p-q)=0
-
 4:03
4:03
.2 (a) if pth, qth, rth term of an a.p. are a, b, c respectively, show that (q-r)a (r-p)b (p-q)...
-
 13:02
13:02
the pth, qth and rth terms of an a.p. are a, b and c respectively. show that a(q – r) b(r - p) c
-
 9:53
9:53
if the pth, qth and rth terms of an a.p. be a, b and c , then prove that a(q−r) b(r−p) c(p−q)=0.
-
 7:40
7:40
in an a.p. if mth term is n and nth term is m where m ≠ n .find the pth term || sequence and series
-
 6:15
6:15
arithmetic sequence | determine the indicated term of an arithmetic sequence | math 10
-
 15:18
15:18
if the coefrth, (r 1)th and (r 2)th (1 x)ⁿ are in a.p., prove n² - (4r 1)n 4r² - 2 = 0.
-
 5:37
5:37
if p, q, r be in arithmetic progression, then show that the pth, qth and rth terms of any geometric
-
 8:51
8:51
if the pth, qth and rth terms of an a.p. be a, b and c respectively. then prove that a(q–r)...
-
 9:00
9:00
if the pth, qth and rth terms of an ap be a, b, c respectively then show that a(q - r) b(r - p)
-
 7:46
7:46
prove if pth, qth and rth terms of an a.p. be a, b and c . a(q–r) b(r–p) c(p–q) = 0. ap class 10
-
 8:32
8:32
if the pth qth and rth terms of an ap be a b c respectively then show that a(q-r) b(r-p) c(p-q)=0
-
 4:47
4:47
if x ,y.z are the pth ,qth are rth term of an a.p... then show that - x(q-r) y(r-p) z(p-q) = 0
-
 6:05
6:05
x a p if a, b, c are the pth , qth and rth terms of an ap, then prove that aq r br p cp q 0
-
 10:03
10:03
problem based pth qth and rth terms
-
 3:42
3:42
pth term of an ap is q and qth term is p, then prove that its nth term is (p q-n).class-10th math ap
-
 7:03
7:03
if pth, qth, rth term of a g.p. are a, b, c respectively. prove that a^(q-r).b^(r-p).c^(p-q)=1
-
 3:07
3:07
the pth, qth, & rth terms of an ap are x,y,z respectively.
-
 9:31
9:31
if pth, qth, rth terms of an a.p. be a, b, c respectively, then prove that a(q-r) b(r-p) c(p-q) =0
-
 3:25
3:25
if the am between pth and qth terms of an ap is equals am between rth and sth term, then p q=r s
Clip.africa.com - Privacy-policy
 9:12
9:12
 5:27
5:27
 7:21
7:21
 4:03
4:03
 13:02
13:02
 9:53
9:53
 7:40
7:40
 6:15
6:15
 15:18
15:18
 5:37
5:37
 8:51
8:51
 9:00
9:00
 7:46
7:46
 8:32
8:32
 4:47
4:47
 6:05
6:05
 10:03
10:03
 3:42
3:42
 7:03
7:03
 3:07
3:07
 9:31
9:31
 3:25
3:25