if `veca,vecb` and `vecc` are three non-coplanar vectors, then the vector equation

Published 4 years ago • 7 plays • Length 1:41

Download video MP4
Download video MP3

Similar videos

6:23

if `veca,vecb,vecc` are three non coplanar vectors then the vector equation `vecr=(1-p-q)
1:57

if `veca,vecb` and `vecc` are three non-coplanar vectors then the length of projection
5:07

if veca vecb,vecc are any three non- coplanar vectors then the equation [vecbxxvecc veccxxveca ...
3:12

if a,b,c are three non-coplanar vector, then the vectors equation r = (1 -p-q) a p b qc`
$if `veca, vecb and vecc` be any three non coplanar vectors. then the system of vectors veca\',vecb\'$ 14:22

if `veca, vecb and vecc` be any three non coplanar vectors. then the system of vectors veca\',vecb\'
1:48

if `veca, vecb, vecc` are non-coplanar vectors then `(veca.vecbxxvecc)/(veccxxveca.vecb) (vecb
10:17

if `veca,vecb and vecc` are three non coplanar vectors and `vecr` is any vector in space, then
8:29

if veca, vecb and vecc are any three non-coplanar vectors, then prove that points l_(1)veca m_(...
4:34

if `veca,vecb,vecc` are non-coplanar vectors than `( veca . vecb xx vecc )/(veccxxveca.vecb)
4:44

if `veca, vecb, vecc` are three non-coplanar vectors, then a vector `vecr` satisfyi
4:24

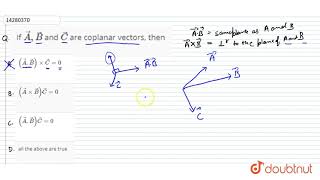
if `veca,vecb` and `vecc` are coplanar vectors, then
2:53

if `vec a, vec c, vec d` are non-coplanar vectors, then `vec d.{vec a xx [vec b xx(vec c xx v
4:59

theorem 2: if `veca`, `vecb` and `vecc` are non coplanar vectors; then any vector `vecr` can be
8:44

`veca,vecb` and `vecc` are three non-coplanar vectors and r is any arbitrary vector. prove that
4:18

if` veca,vecb,vecc` are non coplanar vectors then `([veca 2vecb vecb 2cvecc vecc 2veca])/([veca vecb
2:52

if `veca, vecb` and `vecc` are unit coplanar vectors, then the scalar triple product `[(2v
4:46

if `veca,vecb, vecc` are unit coplanar vectors then the scalar triple product `[2veca-vecb 2vecb
4:03

if veca, vecb, vecc are non-coplanar vectors, prove that the following vectors are coplanar.(i)3...
3:38

if `veca, vecb, vecc` are three non-coplanar vetors represented by non-current edges of a

Clip.africa.com - Privacy-policy