prove that if ∑_n=1^∞ a_n is a convergent series of positive real numbers, then so is…
Published 8 hours ago • No plays • Length 0:33Download video MP4
Download video MP3
Similar videos
-
 5:26
5:26
analysis - convergence of addition, product of a convergent series
-
 0:33
0:33
outline of the proof of the rearrangement theorem a. let ϵbe a positive real number, let l=…
-
 16:18
16:18
convergence and divergence - introduction to series
-
 9:40
9:40
convergence and divergence: the return of sequences and series
-
 1:41:20
1:41:20
mathematical methods (8). real numbers and sequences (part 2)
-
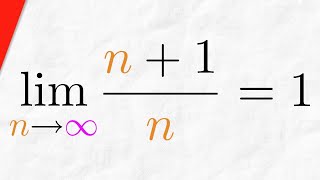 6:43
6:43
proof: sequence (n 1)/n converges to 1 | real analysis
-
 7:24
7:24
proof: limit law for sum of convergent series | real analysis
-
![[proof] infinite series converges](https://i.ytimg.com/vi/kUaT_B2pLqE/mqdefault.jpg) 6:09
6:09
[proof] infinite series converges
-
 6:06:54
6:06:54
100 series convergence tests (no food, no water, no stop)
-
 6:53
6:53
proof: sequence (3n 1)/(n 2) converges to 3 | real analysis
-
 27:54
27:54
sequences | convergence and divergence
-
 3:12
3:12
sequence of natural numbers is divergent
-
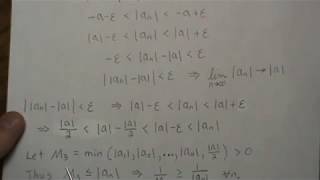 9:26
9:26
bounds on a convergent sequence of real numbers
-
 6:07
6:07
cauchy sequences of real numbers are convergent
-
 15:08
15:08
sequences #theorem#convergent sequences
-
 11:08
11:08
examples of convergent and divergent sequences
-
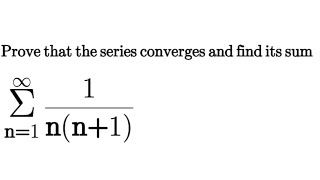 8:31
8:31
prove that the series ∑(1/(n(n 1)) from n=1 to ∞ converges and find its sum
-
 1:11:59
1:11:59
math-s400: lecture iii - convergence of sequences
-
 18:54
18:54
sequences of real numbers
-
 9:59
9:59
proof of the additivity of sequence convergence
-
 5:03
5:03
47 subsequences of convergent sequences part 2
-
 9:38
9:38
reciprocal of a convergent sequence converges to reciprocal of limit provided if limit nonzero