15-20 identify the curve by finding a cartesian equation for the curve. r=3 sinθ
Published 7 days ago • No plays • Length 0:33Download video MP4
Download video MP3
Similar videos
-
13:17
find the area of the curve r=a.sin(3theta)|quadrature|#speak with math
-
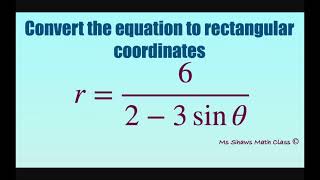2:55
convert polar equation to rectangular equation r= 6/(2 - 3 sin x).
-
5:26
eliminate the parameter to find a cartesian equation of the curve
-
5:59
find area of region that lies inside polar curve r = 2 sin theta and outside curve r = 3 sin theta
-
5:07
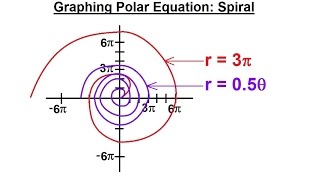
precalculus - polar coordinates (22 of 35) graphing polar eqns: r=3(theta), r=0.5(theta), spiral
-
0:33
identify the curve by finding a cartesian equation for the curve. r^2 sin2 θ=1
-
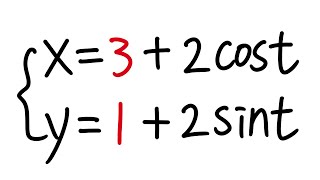4:49
how to convert parametric x=3 2sin(t), y=1 2sin(t) to cartesian
-
3:16
sketch the curve r = -2 sin theta first sketching r as a function of theta in cartesian coordinates
-
5:37
precalculus - polar coordinates (12 of 35) graphing polar equations: r=3, r=3sin(theta), circles
-
5:52
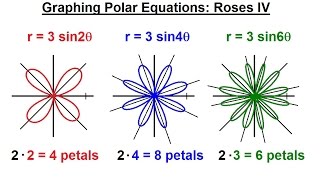
precalculus - polar coordinates (17 of 35) graphing polar equations: r=3sin2(theta), roses
-
![find the area of the loops of the curve r=a.sin3θ.[three leaved rose]](https://i.ytimg.com/vi/RRB-bynA-oQ/mqdefault.jpg)
9:55
find the area of the loops of the curve r=a.sin3θ.[three leaved rose]
-
6:32
find area of region that lies inside polar curve r = 3 cos theta and outside curve r = 1 cos theta
-
8:17
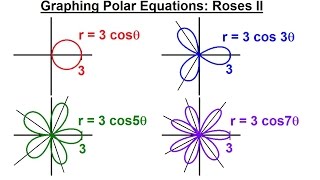
precalculus - polar coordinates (15 of 35) graphing polar equations: r=3cos3(theta), roses
-
13:03
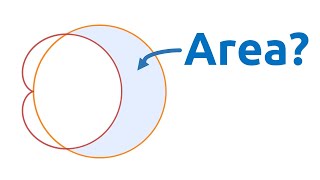
finding the area of the region inside the circle r=3cos(theta) & outside the cardioid r=1 cos(theta)
-
4:09
convert the polar equation r = 5sin(theta) to rectangular and graph
-
6:56
how to find the equation of a plane given three points